Using Ohm’s Law to Build a Voltage Divider

Build Materials (For each team)

Required Materials (all materials can be reused)

• Multimeter 
• Breadboard with Wire Set 
• Calculator 
• LED – Super Red, Clear Lens 
• 9V Alkaline Battery 
• 9V Battery Holder with Wire Leads 
• Resistor: 100 ohm, Carbon Film, 1/2W, 5% 
• Resistor: 150 ohm, Carbon Film, 1/2W, 5% 
• Resistor: 220 ohm, Carbon Film, 1/2W, 5% 
• Resistor: 330 ohm, Carbon Film, 1/2W, 5% 
• Resistor: 470 ohm, Carbon Film, 1/2W, 5% 
• Resistor: 560 ohm, Carbon Film, 1/2W, 5% 
• Resistor: 680 ohm, Carbon Film, 1/2W, 5% 
• Resistor: 820 ohm, Carbon Film, 1/2W, 5% 
• Resistor: 910 ohm, Carbon Film, 1/2W, 5% 
• Resistor: 1000 ohm, Carbon Film, 1/2W, 5%

Materials

• Use build materials

Process

Students test their circuits by lighting up the LED bulb. Students must predict and then measure the output voltage values of their circuits using a multimeter

Design Challenge

You are part of a team of engineers given the challenge of understanding how Ohm’s Law works and applying it. You’ll learn how to read resistor codes, what a breadboard is and how to calculate resistor values. Then, your team will use a breadboard to build a voltage divider circuit that can illuminate a light emitting diode (LED bulb). You must predict and measure with a multimeter the output voltage values of your circuit. 

Criteria 

• Use a breadboard to build a voltage divider circuit
• Use a multimeter to measure the output voltage values

Constraints

• Use only the materials provided.

1. Break class into teams of 2.
2. Hand out the Using Ohm’s Law to Build a Voltage Divider worksheet, as well as some sheets of paper for sketching designs. 
3. Discuss the topics in the Background Concepts Section and Review the Teacher Guide Section. Consider asking students if they know how a circuit works. What happens when you flip a light switch on or off?
   
4. Review the Engineering Design Process, Design Challenge, Criteria, Constraints and Materials. 
5. To prepare for the activity, review the Teacher Appendix 1, 2, and 3 and the Voltage Divider Information Sheet. 
6. Provide each team with their material kits.
7. Instruct students to complete Step 1 – Resistor Color Codes. Students review the handout on Resistor Color Codes and then determine the color codes for the resistors in their material kit. After finding each resistor in the kit, students can measure and record the resistance and determine whether the value is within the tolerance.
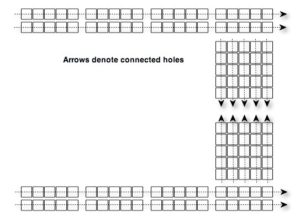
8. Instruct students to complete Step 2 – Understanding Breadboards.  Breadboards normally have rows of holes along each edge that are connected together. Then, running perpendicular to the edge holes, there are shorter rows with holes connected together. Oftentimes, the breadboards are split into two halves so that an integrated circuit can be placed in the middle of the board. For these boards, there will be a set of holes on each side of the split that are connected to each other, but are not connected across the split.Invite students to explore the breadboards found in their kits. In the spaces provided on their worksheets, encourage students to draw diagrams of some of the connections on the breadboards and how the breadboards may be used to build a voltage divider circuit.
   
   Invite students to explore the breadboards found in their kits. In the spaces provided on their worksheets, encourage students to draw diagrams of some of the connections on the breadboards and how the breadboards may be used to build a voltage divider circuit.
9. Instruct students to complete Step 3 – Building a Voltage Divider. Using the diagram and the resistors in the lesson kit, invite students to build a voltage divider using the 9V battery, R1=820ohm, and R2=470ohm. Students can then predict and measure output voltages for their voltage dividers and record the information on their worksheets.
10. Instruct students to complete Step 4 – Building a Voltage Divider for a Desired Output. Using the voltage divider circuit, challenge students to select R1 and R2 from the lesson kit to produce the output voltages listed on their worksheet.
11. Instruct students to complete Step 5 – Building a Light Emitting Diode Circuit. A circuit to illuminate a Light Emitting Diode (LED) is very similar to a Voltage Divider circuit. An LED circuit replaces R1 with the LED. For an LED in this configuration, V1 will be a constant voltage, regardless of the total current. Therefore, for these circuits, V2 is also known. LED’s require a certain amount of current for optimal operation. This is called the bias current. Therefore, if V2 and bias current are known, students can calculate a value for R2.Instruct students to complete the exercises on their worksheets.
    
    Instruct students to complete the exercises on their worksheets.
12. For more content on the topic, see the “Digging Deeper” section.
    

Extension Ideas  

• Create an Excel spreadsheet that predicts all possible output voltages given a selection of resistors and batteries.  
• Remove R2 from the circuit. Replace R1 with the largest available value. Connect the multimeter to measure V2, using the multimeter’s internal resistance instead of R2. Use the voltage measured to calculate the internal resistance of the multimeter.

The lesson can be done in as little as 1 class period for older students. However, to help students from feeling rushed and to ensure student success (especially for younger students), split the lesson into two periods giving students more time to brainstorm, test ideas and finalize their design. Conduct the testing and debrief in the next class period.

• Circuit: A complete path around which electricity can flow
• Constraints: Limitations with material, time, size of team, etc.
• Criteria: Conditions that the design must satisfy like its overall size, etc.
• Engineers: Inventors and problem-solvers of the world. Twenty-five major specialties are recognized in engineering (see infographic).
• Engineering Design Process: Process engineers use to solve problems. 
• Engineering Habits of Mind (EHM): Six unique ways that engineers think.
• Iteration: Test & redesign is one iteration. Repeat (multiple iterations).
• LED: Light Emitting Diode. A semiconductor device that produces light from electricity.
• Multimeter: Electronic measuring tool that is a combination of several tools in one unit.
• Ohm’s Law: The way current flows through a resistance when a different electric potential (voltage) is applied at each end of the resistance.
• Prototype: A working model of the solution to be tested.
• Resistor: Part of an electrical circuit that resists, or limits, the power of an electrical current in a circuit.
• Voltage: Name for the electric force that causes electrons to flow. It’s the measure of potential difference between two points in the circuit.
• Voltage Divider: An electrical circuit which creates an output voltage which is proportional to an input voltage.

Internet Connections

• IEEE Global History Network 
• National Council of Teachers of Mathematics Principles and Standards for School Mathematics  

Recommended Reading

• Ohm’s Law, Electrical Math and Voltage Drop Calculations by Tom Henry. (ISBN: 978-0945495260)  
• Teach Yourself Electricity and Electronics, Fourth Edition (Paperback) by Stan Gibilisco. (ISBN: 978-0071459334)  
• Electrical Engineering 101: Everything You Should Have Learned in School but Probably Didn’t by Darren Ashby. (ISBN: 978-1856175067)

Writing Activity 

Research the life and work of Georg Ohm and write a page on how his discoveries have impacted modern electronics.

Alignment to Curriculum Frameworks 

Note: Lesson plans in this series are aligned to one or more of the following sets of standards:  • U.S. Science Education Standards (http://www.nap.edu/catalog.php?record_id=4962) • U.S. Next Generation Science Standards (http://www.nextgenscience.org/)  • International Technology Education Association’s Standards for Technological Literacy  (http://www.iteea.org/TAA/PDFs/xstnd.pdf) 

• U.S. National Council of Teachers of Mathematics’ Principles and Standards for School  Mathematics (http://www.nctm.org/standards/content.aspx?id=16909) 
• U.S. Common Core State Standards for Mathematics (http://www.corestandards.org/Math) • Computer Science Teachers Association K-12 Computer Science Standards  (http://csta.acm.org/Curriculum/sub/K12Standards.html) 

National Science Education Standards Grades 5-8 (ages 10-14) CONTENT STANDARD A: Science as Inquiry

As a result of activities, all students should develop 

• Abilities necessary to do scientific inquiry  
• Understandings about scientific inquiry  

CONTENT STANDARD B: Physical Science 

As a result of their activities, all students should develop an understanding of ✦ Transfer of energy  

National Science Education Standards Grades 9-12 (ages 15-18) CONTENT STANDARD A: Science as Inquiry

As a result of activities, all students should develop 

• Abilities necessary to do scientific inquiry  
• Understandings about scientific inquiry  

CONTENT STANDARD B: Physical Science  

As a result of their activities, all students should develop understanding of ✦ Interactions of energy and matter  

Next Generation Science Standards Grades 3-5 (Ages 8-11) Energy

Students who demonstrate understanding can: 

✦ 4-PS3-4. Apply scientific ideas to design, test, and refine a device that  converts energy from one form to another. 

Next Generation Science Standards Grades 6-8 (Ages 11-14) Motion and Stability: Forces and Interactions

✦ MS-PS2-3. Ask questions about data to determine the factors that affect the  strength of electric and magnetic forces. 

Next Generation Science Standards Grades 9-12 (Ages 14-18) Energy

✦ HS-PS3-1. Create a computational model to calculate the change in the energy of one component in a system when the change in energy of the  other component(s) and energy flows in and out of the system are known. 

✦ HS-PS3-3. Design, build, and refine a device that works within given  constraint s to convert one form of energy into another form of energy.*

Principles and Standards for School Mathematics (ages 10 – 14) Measurement Standards

• Apply appropriate techniques, tools, and formulas to determine measurements. ✦ use common benchmarks to select appropriate methods for estimating  measurements. 

Principles and Standards for School Mathematics (ages 14 – 18) Measurement Standards

• Understand measurable attributes of objects and the units, systems, and  processes of measurement 
• make decisions about units and scales that are appropriate for problem  situations involving measurement. 
• Apply appropriate techniques, tools, and formulas to determine measurements.
• analyze precision, accuracy, and approximate error in measurement  situations.  
• use unit analysis to check measurement computations. 

Common Core State Standards for School Mathematics Grades 3-8 (ages 8-14) Measurement & Data

• Convert like measurement units within a given measurement system. ✦ CCSS.Math.Content.5.MD.A.1 Convert among different-sized standard  measurement units within a given measurement system (e.g., convert 5 cm  to 0.05 m), and use these conversions in solving multi-step, real world  problems. 

Geometry 

• Graph points on the coordinate plane to solve real-world and mathematical  problems. 

✦ CCSS.Math.Content.5.G.A.2 Represent real world and mathematical problems  by graphing points in the first quadrant of the coordinate plane, and interpret  coordinate values of points in the context of the situation. 

Ratios and Proportional Relationships 

• Understand ratio concepts and use ratio reasoning to solve problems.

✦ CCSS.Math.Content.6.RP.A.3 Use ratio and rate reasoning to solve real-world  and mathematical problems, e.g., by reasoning about tables of equivalent  ratios, tape diagrams, double number line diagrams, or equations. 

✦ CCSS.Math.Content.7.RP.A.2c Represent proportional relationships by  equations. For example, if total cost t is proportional to the number n of  items purchased at a constant price p, the relationship between the total cost  and the number of items can be expressed as t = pn.

 Common Core State Standards for School Mathematics Grades 3-8 (ages 8- 14)

Expressions & Equations 

• Apply and extend previous understandings of arithmetic to algebraic  expressions. 

✦ CCSS.Math.Content.6.EE.A.2 Write, read, and evaluate expressions in which  letters stand for numbers. 

• Reason about and solve one-variable equations and inequalities. 

✦ CCSS.Math.Content.6.EE.B.6 Use variables to represent numbers and write  expressions when solving a real-world or mathematical problem; understand  that a variable can represent an unknown number, or, depending on the  purpose at hand, any number in a specified set. 

✦ CCSS.Math.Content.6.EE.B.7 Solve real-world and mathematical problems by  writing and solving equations of the form x + p = q and px = q for cases in  which p, q and x are all nonnegative rational numbers. 

Functions 

• Define, evaluate, and compare functions. 

✦ CCSS.Math.Content.8.F.A.1 Understand that a function is a rule that assigns  to each input exactly one output. The graph of a function is the set of  ordered pairs consisting of an input and the corresponding output. 

Common Core State Standards for School Mathematics Grades 9-12 (ages 14- 18)

Algebra 

• Create equations that describe numbers or relationships 

✦ CCSS.Math.Content.HSA-CED.A.4 Rearrange formulas to highlight a quantity  of interest, using the same reasoning as in solving equations. For example,  rearrange Ohm’s law V = IR to highlight resistance R. 

• Solve equations and inequalities in one variable. 

✦ CCSS.Math.Content.HSA-REI.B.3 Solve linear equations and inequalities in  one variable, including equations with coefficients represented by letters. 

Standards for Technological Literacy – All Ages

Design 

✦ Standard 10: Students will develop an understanding of the role of  troubleshooting, research and development, invention and innovation, and  experimentation in problem solving. 

The Designed World 

✦ Standard 16: Students will develop an understanding of and be able to select  and use energy and power technologies.

Step by Step Procedures

Step 1: Reading Resistor Values

Before the appropriate resistors can be chosen, their values must be determined. One way, of course, is to measure every resistor. Obviously, this is not practical. Fortunately, every resistor comes with a color-coded value printed on it.

Review the handout on Resistor Color Codes.

Determine the color codes for the following resistors. Find the resistor in the lesson kit. Measure and record the resistance. Is the value within the tolerance?

Step 2: Understanding Breadboards

Engineers often use a tool called a Breadboard to build prototype circuits. Find a white plastic board full of holes and a box of pre-cut wires in the lesson kit. This is the breadboard.

Breadboards are made so that some of the holes are electrically connected, so that circuits can be built. Using the multimeter and wires from the kit of pre-cut wires, draw a diagram of some of the connections on the breadboard.

Next, draw a diagram showing how a voltage divider circuit might be built with the breadboard.

Step 3: Building a Voltage Divider

Using the diagram and the resistors in the lesson kit, build a voltage divider using the 9V battery, R1=820ohm, and R2=470ohm.

What voltage would you expect?

What voltage did you measure?

Step 4: Building a Voltage Divider for a Desired Output

Using the voltage divider circuit, select R1 and R2 from the lesson kit to produce the following output voltages

Step 5: Building a Light Emitting Diode circuit

A circuit to illuminate a Light Emitting Diode (LED) is very similar to a Voltage Divider circuit. An LED circuit replaces R1 with the LED. For an LED in this configuration, V₁ will be a constant voltage, regardless of the total current. Therefore, for these circuits, V₂ is also known. LED’s require a certain amount of current for optimal operation. This is called the bias current. Therefore, if V₂ and bias current are known, a value for R2 can be calculated.

As the name implies, LED’s are diodes and they will only illuminate when installed with the proper polarity. For this circuit, the flatted side should point towards R2

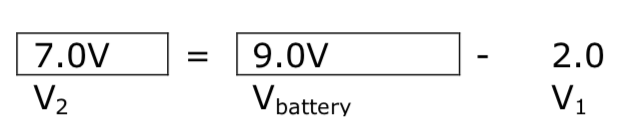
If R1 is replaced with an LED that has a voltage V₁ of 2.0V and requiring a bias current of 20mA, (0.020A) determine the following

What is the value of V₂?

What is the value of I_total

What is the resistor required for proper bias.

Try a few resistors near the calculated value to find an optimal LED brightness.  Measure V₂ and compute the bias current.

Which resistor is the best choice? Why? What happens if the LED is installed backwards?

Lesson Goal

This lesson encourages students to use Ohm’s Law to design and build a voltage divider circuit. The voltage divider is one of the first circuits Electrical Engineering students learn and it is very useful for the study of Ohm’s law and associated concepts.  During this lesson students derive and apply mathematical equations to build voltage divider circuits, including a circuit that will power a light emitting diode (LED).

Lesson Objectives

• Learn about Ohm’s Law.
• Use a digital multimeter to collect data.
• Explore the concepts of voltage and current.
• Analyze the electrical requirements of light emitting diodes (LED’s).

Materials

• Student handouts
• One set of materials for each group of students:
  Note: The following materials list can be adapted for material on hand or for obtaining other voltage outputs.  All materials can be reused.

  Multimeter

  Breadboard with Wire Set

  Calculator

  LED – Super Red, Clear Lens

  9V Alkaline Battery

  9V Battery Holder with Wire Leads

  Resistor: 100 ohm, Carbon Film, 1/2W, 5%

  Resistor: 150 ohm, Carbon Film, 1/2W, 5%

  Resistor: 220 ohm, Carbon Film, 1/2W, 5%

  Resistor: 330 ohm, Carbon Film, 1/2W, 5%

  Resistor: 470 ohm, Carbon Film, 1/2W, 5%

  Resistor: 560 ohm, Carbon Film, 1/2W, 5%

  Resistor: 680 ohm, Carbon Film, 1/2W, 5%

  Resistor: 820 ohm, Carbon Film, 1/2W, 5%

  Resistor: 910 ohm, Carbon Film, 1/2W, 5%

  Resistor: 1000 ohm, Carbon Film, 1/2W, 5%

Time Needed

Three to four 45 minute sessions

Procedure

Divide students into groups of two. Show students the various Student Resource Sheets.  These may be read in class, or provided as reading material for the prior night’s homework.

Step 1: Reading Resistor Values

Students will find each of the following resistors in their lesson kit. They can review the handout on Resistor Color Codes and then determine the color codes for the following resistors. After finding each resistor in the lesson kit students can measure and record the resistance and determine whether the value is within the tolerance.

Step 2: Understanding Breadboards

Breadboards normally have rows of holes along each edge that are connected together. Then, running perpendicular to the edge holes, there are shorter rows with holes connected together. Oftentimes, the breadboards are split into two halves so that an integrated circuit can be placed in the middle of the board. For these boards, there will be a set of holes on each side of the split that are connected to each other, but are not connected across the split.

Invite students to explore the breadboards found in their kits. In the spaces provided on their worksheets, encourage students to draw diagrams of some of the connections on the breadboards and how the breadboards may be used to build a voltage divider circuit.

Step 3: Building a Voltage Divider

Using the diagram and the resistors in the lesson kit, invite students to build a voltage divider using the 9V battery, R1=820ohm, and R2=470ohm. Students can then predict and measure output voltages for their voltage dividers and record the information on their worksheets.

Assuming the 9V battery, R1=820ohm, and R2=470ohm.

What voltage would you expect?

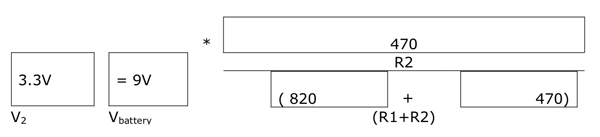
What voltage did you measure?

Remember that the resistors have tolerances!!

Step 4: Building a Voltage Divider for a Desired Output

Using the voltage divider circuit, challenge students to select R1 and R2 from the lesson kit to produce the following output voltages:

Step 5: Building a Light Emitting Diode circuit

A circuit to illuminate a Light Emitting Diode (LED) is very similar to a Voltage Divider circuit. An LED circuit replaces R1 with the LED. For an LED in this configuration, V₁ will be a constant voltage, regardless of the total current. Therefore, for these circuits, V₂ is also known. LED’s require a certain amount of current for optimal operation. This is called the bias current. Therefore, if V₂ and bias current are known, students can calculate a value for R2.

As the name implies, LED’s are diodes. This means that they will only illuminate when installed with the proper polarity. In most cases, the flatted side of the LED needs to face towards the lower voltage. For this circuit, the flatted side should point towards R2

If R1 is replaced with an LED that has a voltage V₁ of 2.0V and requiring a bias current of 20mA, (0.020A) determine the following:

What is the value of V2?

What is the value of I_total

What is the resistor required for proper bias.

Try a few resistors near the required resistor value. Measure V2 and compute the bias current.

V2 measured	Vbattery	R2	I2 calculated
7.0	9.0	220	32mA
7.0	9.0	330	21mA
7.0	9.0	470	15mA

Which resistor is the best choice? Why?

 

Many correct answers are possible, depending on the actual resistor value and the parameters for the particular LED. Students should be encouraged to try different resistors to find a pleasing LED brightness, without being out of specified parameters.

Appendix 1: Equations for Series and Parallel Resistance

By applying basic concepts and Ohm’s Law, the equations for series and parallel resistance can be derived.

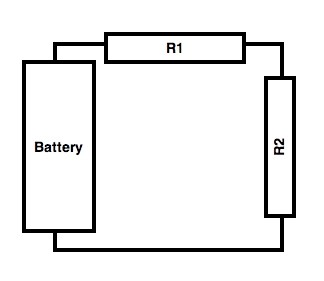
	For a series circuit, R1 is said to be in series with R2. For these circuits, the currentflowing through each device in series is the same. Adding the voltages across each element in series is equal to the total (battery) voltage.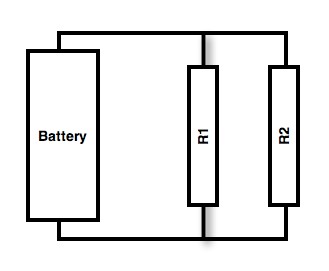
	For a parallel circuit, R1 is said to be in parallel with R2. For these circuits, the voltage across each device in parallel is the same. Adding the current through each element in parallel is equal to the total (battery) current.

These concepts can be used to derive the equations for series and parallel resistors.

Series Resistors

I1 = I2 = Itotal

Vbattery = V1 +V2 V₁ = I₁*R1

V₂ = I₂*R2

Vbattery = Itotal * Rtotal

Substituting, and dividing by I_total

Itotal * Rtotal = I1*R1 + I2*R2

R_total = R1 + R2

 Parallel Resistors

Vbattery = V1 = V2 Itotal = I1 + I2

Substituting, and dividing by V_battery

Vbattery/Rtotal = V1/R1 + V2/R2

1/R_total = 1/R1 + 1/R2

Solving for R_total

R_total = (R1*R2)/(R1+R2)

Appendix 2: Matrix of Possible Voltage Outputs

For the specified list of resistors and a 9V battery, the following output voltages are possible:

Output Voltage	100	150	220	330	470	560	680	820	910	1000
100	4.50	3.60	2.81	2.09	1.58	1.36	1.15	0.98	0.89	0.82
150	5.40	4.50	3.65	2.81	2.18	1.90	1.63	1.39	1.27	1.17
220	6.19	5.35	4.50	3.60	2.87	2.54	2.20	1.90	1.75	1.62
330	6.91	6.19	5.40	4.50	3.71	3.34	2.94	2.58	2.40	2.23
470	7.42	6.82	6.13	5.29	4.50	4.11	3.68	3.28	3.07	2.88
560	7.64	7.10	6.46	5.66	4.89	4.50	4.06	3.65	3.43	3.23
680	7.85	7.37	6.80	6.06	5.32	4.94	4.50	4.08	3.85	3.64
820	8.02	7.61	7.10	6.42	5.72	5.35	4.92	4.50	4.27	4.05
910	8.11	7.73	7.25	6.60	5.93	5.57	5.15	4.73	4.50	4.29
1000	8.18	7.83	7.38	6.77	6.12	5.77	5.36	4.95	4.71	4.50

Appendix 3: Advanced Equations for Voltage Divider Ratios

The ratio of the battery voltage and the desired voltage can be used to determine the goal ratio of the two resistors. Knowing this ratio is very helpful when choosing from a limited selection of resistors.

 

Starting with the Voltage Divider Equation

 

V₂ = V_battery * (R2)/(R1 +R2)

 

The ratio of the voltage is represented by

 

V₂/V_battery = R2/(R1 + R2)

 

Invert the terms and solve for a simpler ratio of resistors

V_battery/V₂ = (R1 +R2)/R2

V_battery/V₂ = (R1/R2) + (R2/R2)

V_battery/V₂ = R1/R2 + 1

(V_battery/V₂) -1 = R1/R2 R1/R2 = (V_battery/V₂) -1

Consider the requirement for a 5V supply, using a 9V battery. Search for two resistors that obey the following proportion.

R1/R2 = (V_battery/V₂) -1

R1/R2 = (9/5) – 1

R1/R2 = 0.8

Using this ratio, it is immediately clear that R1=820 and R2=1000 will produce the desired voltage.

Voltage Divider Information Sheet

A Voltage Divider is used to produce a desired output voltage, using resistors in series.

The output voltage (voltage across R2) is proportional to the ratio of R1 and R2

Using Ohm’s Law, compute the Voltage across R1 and R2 and the total resistance

 

V₁ = I₁*R1 — where V₁ is the voltage across R1, and I₁ is the current through R1

V₂ = I₂*R2 — where V₂ is the voltage across R2, and I₂ is the current through R2

V_battery = I_total * R_total — where V_battery is the battery voltage and R_total is the total resistance

 

Since R1 and R2 are in series, the total resistance is known.

 

Rtotal = R1 + R2

 

Since R1 and R2 are in series, the current through each resistor is the same as the total current

Itotal = I1 = I2

Solving for V₂

I₂ = V₂/R2

Itotal = Vbattery/Rtotal = Vbattery/(R1+R2)

I2 = Itotal

V₂/R2 = V_battery/(R1 +R2)

V₂ = V_battery(R2/(R1+R2))

Therefore, the voltage across R2 can be determined by controlling the ratio of R2 to the total resistance, R1 + R2.

• Arabic
• Swahili