Binary Basics

Build Materials

Required Materials

• 10 Sheets of 8 ½” x 11” blank paper
• 5 Chairs

Design Challenge

You are a team of engineers given the challenge of learning about binary numbers. You will complete some activities and then a challenge.

Criteria

• Complete 6 activities and 1 challenge.

Constraints

• Use only the materials provided.

1. Break class into teams of 2. It is suggested that, for the younger students, aged between 8 and 10, three sessions of 45 minutes each should be sufficient. For older students, two sessions should be enough).
2. Hand out the Binary Basics worksheet.
3. Discuss the topics on the Student Resources sheet. Then, complete 6 activities and 1 challenge. Discuss what a quandary is:
   
   A Quandary
   Who knows what a quandary is? Does your neighbor know? A quandary was what a distant early cousin of the Flintstones was in when he caught 11 fish. He was really pleased, but on the way home he began to wonder how he could explain eleven fish when he didn’t have enough fingers. Roman Numbers Despite all the wonderful things the Romans did, they were really out to lunch when it came to even simple arithmetic. They had no numbers of any sort and had to use letters.

For example, 2016 comes out as:

MMXVI, which is: 1000+1000+10+5+1

How do you multiply: XI by C?

Even an abacus can’t do that.

And if you are still having difficulty, go have a look at your town clock. Chances are it has Roman Numerals.

P.S. There are charts on the Net which help you convert from Roman to our numbers which actually are Arabic.

A Little Background

Yes, the Romans built the Coliseum and wonderful temples. But only after much trial and error.

Building everyday buildings more than about 3 floors was a challenge because there was no easy way to do simple sums.

Roman history books are full of accounts of ordinary houses falling down.

So today we write all our letters starting on the left and moving to the right. But have you noticed that when we write numbers, we start on the RIGHT, and as they get bigger, we move over to the LEFT.

Notice:

1

10

100

1000

10000

Binary numbers work the same way.

WHAT DO YOU SEE HERE?

Now Visualize a row of 5 Gumball Machines

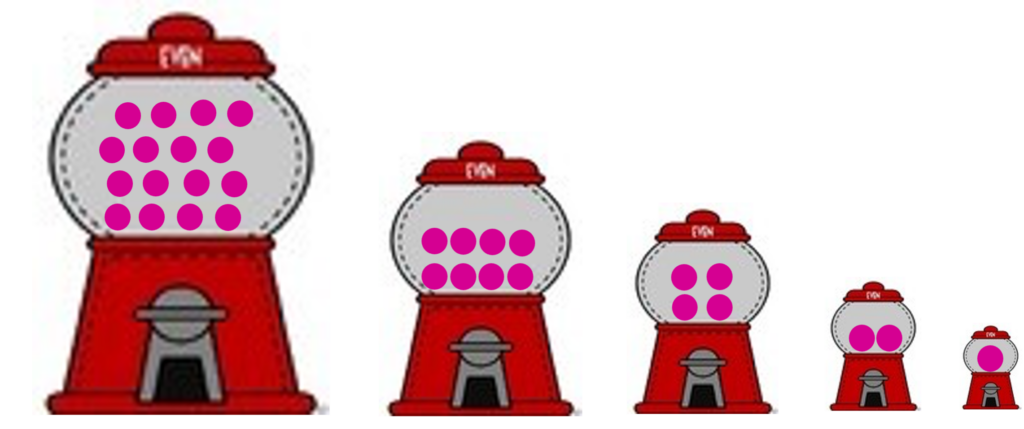
• The one on the far right is very small and can only hold 1 gumball (max)
• The next one to the left is twice as big and can hold 2 gumballs (max)
• Once more to the left is a machine twice as big again. It can hold 4 gumballs.
• After that comes a machine capable of holding twice as many again, or 8 gumballs.
• Finally, the last machine in our line is a jumbo that can hold twice as many as the one before it, or 16 gumballs.

Each of these machines has a flap at the bottom, so that when you pull the lever, ALL the gumballs in that machine fall out.

In other words, these machines are always either completely full, or completely empty.

Now, you might be wondering “If gravity is emptying these machines – how are they filling back up exactly?”

This is not a problem, because there is a small person behind the scenes happy to refill the machines for us – but only when told to do so!

So What Do We Have?

A row of five machines capable of holding gumballs as follows:

Now assuming all our machines are full, how many gumboils do we have?

16 + 8 + 4 + 2 + 1 = 31

Assume the middle machine is empty; how many do we have?

16 + 8 + 0 + 2 + 1 = 27

Assume the left-hand machine and the middle one are empty; what do we have?

0 + 8 + 0 + 2 + 1 = 11

Assume only the first two machines are empty, we would have

0 + 0 + 4 + 2 + 1 = 7

It would help our small person if each of our gumball machines had two flags.

HOW MIGHT THESE FLAGS HELP OUR SMALL PERSON?

Turn and share your thoughts with a partner. Why use the flags? Do you agree?

NOW WHAT DO WE HAVE?

Think about our row of 5 gumball machines, each of which has a “0” flag or a “1” flag

If all machines are full, we would see five flags showing a “1” like this:

Which means we have 31 gumballs

If the middle machine is empty, we would see:

Which means we have 27 gumballs

And if the two machines on the left are empty we would see:

How many gumballs do we have now???

Explain how you know to a partner.

Binary Chairs Challenge

1. Take 5 chairs and line them up.
2. Take 5 sheets of 8-1/2 x 11 paper.
3. Take a felt pen and write a “1’, a “2”, a “4” an “8” and a “16” on them (one on each sheet).
4. Stick the sheet with “1” on it, on the back of the chair on the extreme RIGHT.
5. Then moving over to LEFT, stick the sheets with “2”, “4”, “8” and “16” on the corresponding chairs.
6. In other words, when you have finished, you will have 16, 8, 4, 2, and 1 on the backs of the chairs.
7. Take 5 students at random and seat one student on each of the chairs.
8. Take 5 more sheets of paper and on one side of EACH sheet mark a “1.”
9. Then turn each sheet over and put a “0” on EACH sheet.
10. Give one of these sheets of paper to each of the 5 students.
11. Sit all the other students facing the five mentioned above.
12. Have each of the 5 selected students hold up their piece of paper in any order they like.

Suppose they come up looking like this

Then have the 5 seated students rearrange their papers in some other order, such as:

How does a computer use binary numbers to make the letters of our alphabet?

Turn and talk to a partner about your prediction.

They use a system of 26 coded numbers.

Note 1:  The leading “010” above indicates an upper case letter.  It is shown in bold here simply for ease of identification.

Note 2:  A leading “011” would indicate a lower case letter.

Note 3:  For example, “C”, which is No. 3 in the alphabet is also 3 in binary. “Z”, which is No. 26 in the alphabet, is also 26 in binary terms, which figures.

NOW TRANSLATE THE FOLLOWING MESSAGE, USING THE TABLE ON YOUR HANDOUT 01000001

01001001
01010011

01000110
01001111
01010010

01000001
01010000
01010000
01001100
01000101

SO NOW YOU CAN SEND CODED MESSAGES TO YOUR FRIENDS

01001000, 01000001, 01010110, 01000101   

01000001   

01001110, 01001001, 0100011, 01000101

01000100, 01000001, 01011001   !

TRY IT!

TURN YOUR HANDOUT OVER AND WRITE A MESSAGE TO A FRIEND IN BINARY CODE

(use a complete sentence with several words) ***Consider using a number as well  (smaller than 100 please)

WHEN WE’RE FINISHED WE’LL TRADE AND DECODE!!!

How many numbers can a computer store? 

WHY ARE BINARY NUMBERS SO USEFUL?

Despite what you might think, computers are really not smart.  All they do is look for zeros and ones, time after time after time.

And of course, computers never get tired, never take coffee breaks, and (usually) never make mistakes.

The smart part comes with the people who write the “Computer Code” which organizes the zeros and ones into something meaningful.

AN HISTORICAL NOTE

Who has not heard of the “Morse Code”?

• Although not a binary system, there are certain similarities.
• It was developed by Samuel Morse in 1845, as a system of sending messages electrically over long distances by wire.
• This was found to be of great use to the railroads, and in 1866 for sending messages across the Atlantic via submarine cable. Later still it was used by Marconi (1901) for sending messages by radio.  In some cases it is still in use today.
• To each of the 26 letters of the alphabet, Morse allocated a group of three electric pulses, some short and others long, formed by the operator holding down his “key” for long or short periods of time.
• The most famous Morse Code group of letters is S O S, which amongst ships in distress stands for “Save our Souls”.

S is dot dot dot.
O is  dash dash dash.
S is  dot dot dot.
Or  … _ _ _ … Easy to remember and easy to do.

• An early application was when the Titanic sank in 1912.
• The full Morse Code is available on the net.
• The first message sent by Morse in 1845 was “What Hath God Wrought”.
• He was also a famous portrait painter, which shows you don’t have to be a specialist.

The lesson can be done in as little as 1 class period for older students. However, to help students from feeling rushed and to ensure student success (especially for younger students), split the lesson into two periods giving students more time to brainstorm, test ideas and finalize their design. Conduct the testing and debrief in the next class period.

Why Are Binary Numbers so Useful?

Despite what you might think, computers are really not smart. All they do is look for zeros and ones, time after time after time.

And of course, computers never get tired, never take breaks, and (usually) never make mistakes.

The smart part comes with the people who write the “Computer Code” which organizes the zeros and ones into something meaningful.

Morse Code

Who has not heard of the “Morse Code”?

• Although not a binary system, there are certain similarities.
• It was developed by Samuel Morse in 1845, as a system of sending messages electrically over long distances by wire.
• This was found to be of great use to the railroads, and in 1866 for sending messages across the Atlantic via submarine cable. Later still it was used by Marconi (1901) for sending messages by radio. In some cases it is still in use today.
• To each of the 26 letters of the alphabet, Morse allocated a group of three electric pulses, some short and others long, formed by the operator holding down his “key” for long or short periods of time.

The most famous Morse Code group of letters is S O S, which amongst ships in distress stands for “Save our Souls.”

S is dot dot dot.

O is dash dash dash.

S is dot dot dot.

Or … _ _ _ … Easy to remember and easy to do.

• An early application was when the Titanic sank in 1912.
• The full Morse Code is available on the net.
• The first message sent by Morse in 1845 was “What Hath God Wrought”.
• He was also a famous portrait painter, which shows you don’t have to be a specialist.

Internet Connections

• ITEA Standards for Technological Literacy
• NSTA National Science Education Standards (www.nsta.org/publications/nses.aspx)

Writing Activity

Having discussed the obvious limitations of this very simple demonstration, students should be asked to set out ways in which they think it could be improved.

Alignment to Curriculum Frameworks

Note: Lesson plans in this series are aligned to one or more of the following sets of standards:

• S. Science Education Standards (http://www.nap.edu/catalog.php?record_id=4962)
• S. Next Generation Science Standards (http://www.nextgenscience.org/)
• International Technology Education Association’s Standards for Technological Literacy (http://www.iteea.org/TAA/PDFs/xstnd.pdf)
• S. National Council of Teachers of Mathematics’ Principles and Standards for School Mathematics (http://www.nctm.org/standards/content.aspx?id=16909)
• S. Common Core State Standards for Mathematics (http://www.corestandards.org/Math)
• Computer Science Teachers Association K-12 Computer Science Standards (http://csta.acm.org/Curriculum/sub/K12Standards.html)

National Science Education Standards Grades K-4 (ages 4 – 9)

CONTENT STANDARD A: Science as Inquiry

As a result of activities, all students should develop

• Abilities necessary to do scientific inquiry

CONTENT STANDARD B: Physical Science

As a result of the activities, all students should develop an understanding of

• Light, heat, electricity, and magnetism

CONTENT STANDARD E: Science and Technology

As a result of activities, all students should develop

• Abilities of technological design
• Understanding about science and technology

National Science Education Standards Grades 5-8 (ages 10 – 14)

CONTENT STANDARD A: Science as Inquiry

As a result of activities, all students should develop

• Understandings about scientific inquiry

CONTENT STANDARD B: Physical Science

As a result of their activities, all students should develop understanding of

• Interactions of energy and matter

CONTENT STANDARD E: Science and Technology

As a result of activities, all students should develop

• Abilities of technological design
• Understandings about science and technology

CONTENT STANDARD F: Science in Personal and Social Perspectives

As a result of activities, all students should develop understanding of

• Science and technology in local, national, and global challenges

CONTENT STANDARD G: History and Nature of Science

As a result of activities, all students should develop understanding of

• Historical perspectives

National Science Education Standards Grades 9-12 (ages 14-18) 

CONTENT STANDARD A: Science as Inquiry

As a result of activities, all students should develop

• Understandings about scientific inquiry

CONTENT STANDARD E: Science and Technology

As a result of activities, all students should develop

• Abilities of technological design
• Understandings about science and technology

CONTENT STANDARD F: Science in Personal and Social Perspectives

As a result of activities, all students should develop understanding of

• Personal and community health
• Science and technology in local, national, and global challenges

CONTENT STANDARD G: History and Nature of Science

As a result of activities, all students should develop understanding of

• Historical perspectives

CONTENT STANDARD E: Science and Technology

As a result of activities, all students should develop

• Abilities of technological design
• Understandings about science and technology

CONTENT STANDARD F: Science in Personal and Social Perspectives

As a result of activities, all students should develop understanding of

• Environmental quality
• Natural and human-induced hazards
• Science and technology in local, national, and global challenges

CONTENT STANDARD G: History and Nature of Science

As a result of activities, all students should develop understanding of

• Historical perspectives

Principles and Standards for School Mathematics

Number and Operations Standard
As a result of activities, all students should develop

• Understand numbers, ways of representing numbers, relationships among numbers, and number systems.
• Compute fluently and make reasonable estimates.

Connections Standard

As a result of activities, all students should develop

• Understand how mathematical ideas interconnect and build on one another to produce a coherent whole.
• Recognize and apply mathematics in contexts outside of mathematics.

Standards for Technological Literacy – All Ages

The Nature of Technology

• Standard 3: Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.

Technology and Society

• Standard 7: Students will develop an understanding of the influence of technology on history.

Design

• Standard 9: Students will develop an understanding of engineering design.

The Designed World

Standard 17: Students will develop an understanding of and be able to select and use information and communication technologies.