Fun with Sorting

Build Materials (For each team)

Required Materials

• Cardboard or Construction Paper
• 1 Large marker
• Tape
• Large plastic play blocks
• Large cardboard boxes

Design Challenge

You are part of a team of engineers given the challenge of sorting objects in a list by asking specific questions, like comparing two objects by their numerical value.

Criteria

• Objects with a hidden number will form the list.
• Must sort lists by asking a series of questions.

Constraints

• Numbers are only visible to the “controller”.

1. Break class into teams of 3-5.
2. Hand out the Fun with Sorting worksheet, if you would like the students to complete the questions on the worksheet. Otherwise, you can conduct the activity without the worksheet.
3. Refer to the Background Concepts Section for Tips and Troubleshooting.
4. There is a Basic Sort and then four activities. Activity #2 & #3 should be completed together. And, Activity #3 & #4 should be completed together. Each of them are estimated to take 90 minutes.
5. Review the Basic Sort Instructions below with the class and have students do the Basic Sort Activity.
   Basic Sort Instructions:
   ● Step 1: Students will choose 8 objects to represent the list to be sorted. They may pick anything to represent their list of numbers. Some ideas for the list are: a. Large plastic play blocks b. Large cardboard boxes
   ● Step 2: Students pick one person on the team to be the “controller.”
   ● Step 3: The controller should write random numbers on a piece of paper and tape them to the objects so that they are hidden from the other students. Only the controller should be able to see them.
   ● Step 4: The team will now attempt to sort the list in ascending order. To do this, the students can do these three things:
   a. Ask the controller “Is this number larger than that number?” which allows students to compare any two numbers. The controller may only reply with a yes or a no.
   b. Ask the controller to swap any two objects. The controller will then swap the objects, making sure not to reveal the numbers on them.
   c. Ask the controller to move any object to a specific position, i.e. “Move this object to the third position” or “Move this object in between those two objects.”
   ● Step 5: The controller will keep a count of the number of yes/no questions asked. The students should attempt to sort the numbers while keeping the question count to a minimum.
   ● Step 6: Once the students feel that the list is sorted, they will ask the controller to reveal the numbers. If the list is not sorted, then the controller shuffles up the list and starts over.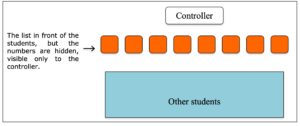
6. Review Activity #1 – Single Insertion Sort Instructions below with the class and have students do a Single Insertion Sort.
   Activity #1 – Single Insertion Sort Instructions:
   ● Step 1: Using blocks or boxes, set up the initial list as follows: one of the numbers should be singled out, and the rest should be pre-arranged in an ascending order. The singled-out number should then be placed at one end of the sorted part of the list. The team should not see the numbers but should know that the entire list is sorted, except for one number at the end, which is out of place.
   
   ● Step 2: The students should then follow the instructions in Step #4 outlined in the Basic Sort above, and attempt to completely sort the list. This is called Single Insertion, and helps as a basic building block for other sorting algorithms like Insertion Sort.
   ● Step 3: Explain to students that if they could see the numbers, it would be obvious that they can simply place 4 between 3 and 5, and the list would be completely sorted. However, that is not the way computers work. Therefore, the students must start off with comparing numbers, and then ordering swaps and/or moves. In this case, the students know that the entire list is in ascending order, except for the last number. The students should naturally realize that they simply need to identify the position in which to insert the last unordered number. INSERT 6 EXAMPLE IMAGES HERE
   The above sequence of diagrams shows what should ideally happen in the classroom. Throughout the activity, the students aren’t aware of the numbers on the list, and simply give a set of instructions to the controller to compare numbers.
   This activity introduces students to the concept of iteration. Iteration is a step in the Engineering Design Process. Students need to iterate over and over again to sort the numbers correctly.
7. Review Activity #2 – Insertion Sort Instructions below with the class and have students do an Insertion Sort.
   Activity #2 – Insertion Sort Instructions:
   ● Step #1: Using blocks or boxes, arrange the list randomly.
   ● Step #2: The students should now attempt to sort it using their prior knowledge of Single Insertion.
   ● Step #3: Students should break down the problem into a series of Single Insertions. A lone number by itself is a sorted list. For instance, we can say that the single number on the extreme left of the randomly arranged list is a sorted list.
   ● Step #4: Students should now consider this 1-element sorted list, and do an Insertion Sort treating the second element as being the out-of-place number in Single Insertion.
   ● Step #4: Once done, students now have a 2-element sorted list. The procedure is then repeated treating the third element as the out-of-place number, so that we get a 3-element sorted list.
   ● Step #5: Students keep on repeating this sequence of Single Insertions, until they finally get the entire sorted list.The following sequence of diagrams show what the students should ideally attempt. Notice how the yellow box, which denotes the sorted portion of the list, grows over time. Note that Single Insertion is carried out repeatedly using the yellow part of the list as the sorted list, and the next element on the right as the out-of-place number. The procedure will eventually sort the whole list!
   INSERT 10 EXAMPLE IMAGES HERE
8. Review Activity #3 – Two-List Merge Sort Instructions below with the class and have students do a Two-List Merge Sort.
   Activity #3 – Two-List Merge Sort Instructions:
   ● Step #1: Set up the initial list as follows: Divide the 8 objects into 2 lists of 4 objects each, and the two lists should be independently sorted.
   ● Step #2: The lists should then be placed side by side, and the students should now attempt to “merge” the two sorted lists into one sorted list by following the instructions from the Basic Sort.
   ● Step #3: This sort is a useful starting point and building block for a more sophisticated algorithm: Merge Sort. This also requires students to recall and reuse their knowledge of Single Insertion.
   ● Step #4: The list on the left is sorted, so you can treat the 5th number as the out-of-place number and sort it within the left list. However, there is something that the students must discover for themselves. They must take advantage of the fact that the list on the right is also sorted, so the next number to be inserted is always greater than the last number inserted.
   ● Step #5: When the students want to merge the second element in the right list into the left list, they do not need to re-run Single Insertion from the extreme left, but simply start from the point at which they inserted the last element.
   INSERT 3 EXAMPLE IMAGES HERE Note that in the step above, you do not start the questions all over from the start of the yellow list, which is what was done in Insertion Sort. This is because we know that the next number to be inserted in the yellow list is already larger than the number inserted last, since the pink list was already sorted.INSERT 4 EXAMPLE IMAGES HERE
9. Review Activity #4 – Merge Sort Instructions below with the class and have students do an Insertion Sort.
   Activity #4 – Merge Sort Instructions:
   ● Step #1: Set-up the list randomly. The students should attempt to sort the list using their previous knowledge of Two-List Merge.
   ● Step #2: The main idea behind Merge Sort is the principle of Divide and Conquer. It is one of the fundamental concepts behind every modern-day sophisticated sorting algorithm. The students will need to consider each number as an individual sorted list of size 1.
   ● Step #3: From there, students will attempt to perform the known Two-List merge on the lists. However, at first sight, what students will attempt will not be very different from Insertion Sort. They will first merge two numbers and then a third and then a fourth, and so on. This is essentially Insertion Sort.
   ● Step #4: The trick to Merge Sort is the following:
   ○ From the randomized list, treat every number as a sorted list of size 1.
   ○ Then, form pairs of adjacent lists and merge them, so that we now have 4 sorted lists, each of size 2.
   ○ Then, form list pairs again and merge, to get 2 lists, each of size 4.
   ○ One final merge, and we get a complete sorted list of size 8. This approach ensures that iterations over each individual number are minimized, so the number of yes/no questions asked is also minimized.
10. For more content on the topic, see the “Digging Deeper” section.

The lesson can be done in as little as 1 class period for older students. However, to help students from feeling rushed and to ensure student success (especially for younger students), split the lesson into two periods giving students more time to brainstorm, test ideas and finalize their design. Conduct the testing and debrief in the next class period.

Tips and Troubleshooting

Throughout the exercises, students should be given every opportunity to come up with the answers themselves. The purpose of the game is for students to “play around” with the problem and see for themselves what works and what doesn’t. This form of discovery-based learning is extremely effective at developing students’ high-level cognitive reasoning and problem-solving skills. Discussions among students should also be encouraged.

Drawing  pictures and diagrams can be highly effective in communicating this particular topic to the students. The graphics provided in the Activity Instructions Section can be used as a guide on how to draw the different steps. Students can also be encouraged to draw diagrams depicting their proposed algorithms and solutions.

If students are having difficulty getting started, here are some tips on how to get students on the right track:

• Encourage students to discuss the task at hand. More often than not, students will inadvertently come up with solutions themselves, when they “think out loud” and discuss the problem and/or its solution with their peers.
• Jump-start the discussion by asking students about their viewpoints, and encouraging students with differing viewpoints to engage in active discussions.
• Offer a potential solution and ask students what they think would happen if it were to be tried. Such a question will most likely trigger a new thought process in the students’ minds, and help them see where they were getting off track. The question itself might refer to what the class was already discussing, or it could be an entirely new, but not necessarily correct thought. The aim is not to provide the correct answer, but encourage students to evaluate possible solutions and think and reason for themselves.

Utilize the inter-team competitions effectively. Try and draw a correlation between the number of questions asked versus the time taken to sort the list, and whether there was a correlation between winning and asking fewer questions.

Internet Connections

• Sorting Algorithm Animations

Recommended Reading

• Art of Computer Programming, Volume 3 by Donald E. Knuth (ISBN: 0321751043)

Writing Activity

Computers generally tend to spend about a full quarter of their processing power on sorting different data. As an example, a computer in a hospital may maintain a very large database of all patients who have ever been to the hospital for treatment in the past 5 years. Different people in the hospital might want different lists of patients. A person managing hospital finances might want a list of patients ordered by their hospital charges. A researcher might want a list ordered by the disease for which they were treated. An administrator might want a list ordered by the doctor who treated the patient. While generating these lists, the computer will have to sort the data afresh every time according to the need of the user. Can you think of any other scenario in which sorting is important? What advantages are there of maintaining sorted data over unsorted data? What are the possible disadvantages?

Alignment to Curriculum Frameworks

Note: Lesson plans in this series are aligned to one or more of the following sets of standards:  

• U.S. Science Education Standards (http://www.nap.edu/catalog.php?record_id=4962)
• U.S. Next Generation Science Standards (http://www.nextgenscience.org/) 
• International Technology Education Association’s Standards for Technological Literacy (http://www.iteea.org/TAA/PDFs/xstnd.pdf)
• U.S. National Council of Teachers of Mathematics’ Principles and Standards for School Mathematics (http://www.nctm.org/standards/content.aspx?id=16909)
• U.S. Common Core State Standards for Mathematics (http://www.corestandards.org/Math)
• Computer Science Teachers Association K-12 Computer Science Standards (http://csta.acm.org/Curriculum/sub/K12Standards.html)

National Science Education Standards Grades K-4 (ages 4 – 9)

CONTENT STANDARD A: Science as Inquiry

As a result of activities, all students should develop

• Abilities necessary to do scientific inquiry 

CONTENT STANDARD B: Physical Science

As a result of the activities, all students should develop an understanding of

• Properties of objects and materials 

CONTENT STANDARD E: Science and Technology 

As a result of activities, all students should develop

• Abilities of technological design 
• Understanding about science and technology 

CONTENT STANDARD F: Science in Personal and Social Perspectives

As a result of activities, all students should develop understanding of

• Types of resources 
• Science and technology in local challenges 

CONTENT STANDARD G: History and Nature of Science

As a result of activities, all students should develop understanding of

• Science as a human endeavor 

National Science Education Standards Grades 5-8 (ages 10 – 14)

CONTENT STANDARD A: Science as Inquiry

As a result of activities, all students should develop

• Abilities necessary to do scientific inquiry 
• Understandings about scientific inquiry 

CONTENT STANDARD B: Physical Science

As a result of their activities, all students should develop an understanding of

• Properties and changes of properties in matter 

CONTENT STANDARD E: Science and Technology

As a result of activities in grades 5-8, all students should develop

• Abilities of technological design 
• Understandings about science and technology 

National Science Education Standards Grades 5-8 (ages 10 – 14) (cont.)

CONTENT STANDARD F: Science in Personal and Social Perspectives

As a result of activities, all students should develop understanding of

• Risks and benefits 
• Science and technology in society 

Principles and Standards for School Mathematics (ages 6 – 18)

Measurement

• understand measurable attributes of objects and the units, systems, and processes of measurement. 
• apply appropriate techniques, tools, and formulas to determine measurements. 

Problem Solving

• build new mathematical knowledge through problem solving.
• solve problems that arise in mathematics and in other contexts.
• apply and adapt a variety of appropriate strategies to solve problems. 
• monitor and reflect on the process of mathematical problem solving. 

Connections

• recognize and apply mathematics in contexts outside of mathematics.

Representation

• create and use representations to organize, record, and communicate mathematical ideas. 
• select, apply, and translate among mathematical representations to solve problems. 

Standards for Technological Literacy – All Ages

The Nature of Technology

• Standard 1: Students will develop an understanding of the characteristics and scope of technology.
• Standard 3: Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.

Technology and Society

• Standard 4: Students will develop an understanding of the cultural, social, economic, and political effects of technology.
• Standard 6: Students will develop an understanding of the role of society in the development and use of technology.

Design

• Standard 9: Students will develop an understanding of engineering design.

Standards for Technological Literacy – All Ages (cont.)

Abilities for a Technological World

• Standard 13: Students will develop abilities to assess the impact of products and systems.

The Designed World

• Standard 14: Students will develop an understanding of and be able to select and use medical technologies.
• Standard 19: Students will develop an understanding of and be able to select and use manufacturing technologies.

Session 1 – Insertion Sort

This is a group exercise. Before starting, please form a group of 3-5 students.

Single Insertion

Draw up 8 cards, each with a different number. Have one student in your group be the controller, and the others should play along. Only the controller is allowed to see the numbers.

The controller should set up the cards for Single Insertion, and the others should play to sort the list. Do this at least 5 times, and fill up the table below.

 

Round	Number of yes/no questions asked	What was the out-of-place number?
1
2
3
4
5

Based on the information you entered above, answer the following questions:

1. What is the average number of questions asked in one round?

 

______________________

 

2. Assume that you were to fill up the table above for 5000 Single Insertions. What do you think would be the largest possible value in the second column (The number of yes/no questions asked)?

 

______________________

 

3. Assume that you were working with a list of 10 numbers instead of 8. What would be your answer to Question 2 in that case?

 

______________________

 

4. Can you now relate the size of the list to the number of questions asked in the worst case? Give a very brief answer about how you think the size of the list and the questions asked in the worst case (Remember, the fewer the number of questions, the better. So when we say “worst case”, we mean the largest possible number of questions asked)

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

 

Insertion Sort

Now, with those same cards, play the Insertion Sort game. Remember to start off with a completely random list.

Do Insertion Sort at least 5 times, and fill out the table below. The controller should keep a record of the third column before starting the sorting, and reveal it after the list has been sorted.

 

Round	Number of yes/no questions asked	What was the starting list?
1
2
3
4
5

 

Based on the information you entered above, answer the following questions:

1. What is the average number of questions asked in one round?

 

______________________

 

2. You must have realized that Insertion Sort is just a series of Single Insertions. Give a very brief answer about how you would relate the number of Single Insertions with the size of the list to be sorted.

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

 

3. Remember your answer to Question 2 from the Single Insertion exercise. Use that answer to calculate the number of questions you would need to ask in Insertion Sort in the “worst case”. Show your steps.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Final Answer: __________________

 

4. Go head-to-head with another group in a sorting match to see who can sort a randomized list faster. There will be one controller from each team, in the interest of fairness. The game rules should be strictly followed, but you may use any procedure you want.

 

Number of questions you asked: _______________________

 

Number of questions your opponent asked: _______________________

 

Did you win? _______________________

 

Session 2 – Merge Sort

This is a group exercise. Before starting, please form a group of 3-5 students.

Two-List Merge

Draw up 8 cards, each with a different number. Have one student in your group be the controller, and the others should play along. Only the controller is allowed to see the numbers.

The controller should set up the cards for Two-list Merge, and the others should play to sort the list. Do this at least 5 times, and fill up the table below.

 

Round	Number of yes/no questions asked	What was the starting list?
1
2
3
4
5

 

Based on the information you entered above, answer the following questions:

1. What is the average number of questions asked in one round?

 

______________________

 

2. Assume that you were to fill up the table above for 5000 Two-list Merges. What do you think would be the largest possible value in the second column (The number of yes/no questions asked)?

 

______________________

 

3. Assume that you were working with a list of 10 numbers instead of 8. What would be your answer to Question 2 in that case?

 

______________________

 

4. Now go back and have a look at the answers you gave for the exercise on Single Insertion. What similarities do you see? What differences? How do the numbers vary? Do they vary a little, or do they vary a lot? Write down your thoughts on this.

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

__________________________________________________________________

 

Merge Sort

Now, with those same cards, play the Merge Sort game. Remember to start off with a completely random list.

Do Merge Sort at least 5 times, and fill out the table below. The controller should keep a record of the third column before starting the sorting, and reveal it after the list has been sorted.

 

Round	Number of yes/no questions asked	What was the starting list?
1
2
3
4
5

 

Based on the information you entered above, answer the following questions:

1. What is the average number of questions asked in one round?

 

______________________

 

2. You must have realized that Merge Sort is just a series of Two-list Merges. How many Two-list Merges did you do to Merge Sort the list of 8 numbers?

 

______________________

 

3. Remember your answer to Question 2 from the Two-list Merge exercise. Use that answer to calculate the number of questions you would need to ask in Merge Sort in the “worst case”. Show your steps.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Final Answer: __________________

 

4. Go head-to-head with another group in a sorting match to see who can sort a randomized list faster. There will be one controller from each team, in the interest of fairness. The game rules should be strictly followed, but you may use any procedure you want.

 

Number of questions you asked: _______________________

 

Number of questions your opponent asked: _______________________

 

Did you win? _______________________

Lesson Plan Translation

[language-switcher]