Kompleksiteit - It is simpel

Bouwmaterialen

Fereaske materialen

• Karton om nûmere kaarten te meitsjen, as ferskate dekken spylkaarten (3 per studint)
• Beloningsartikelen: Rice, lytse snoepjes as oare goedkeape items. As rys as foarbyld nimme, binne sawat 25 eetlepels nedich (dit is in bytsje minder dan 400g)

Tarieding

Meitsje kaarten fan karton of papier en nûmere se sekwinsjoneel begjinnend mei 1. Trije kaarten per studint binne fereaske. As alternatyf kinne twa as trije dekken spylkaarten wurde brûkt, mar de folchoarder fan 'e kaarten moat wurde útlein foar de studinten.

Design Challenge

Jo binne in yngenieur sjoen de útdaging om algoritmen te analysearjen, te ûntwikkeljen en út te fieren mei spultsjes.

1. Diel it wurkblêd Complexity It's Simple út. It begryp fan 'e side "Groei fan sekwinsjes" is essensjeel foar de rest fan' e les. Testje it begryp fan it materiaal. De oplossing wurdt hjirûnder werjûn:
   

   Oplossing
   

   Pompeblêden 9 wiken. Sûnt it oantal lelies elke wike ferdûbelet, as de fiver op 9 wiken healwei bedekt is, wurdt it nei 10 wiken folslein bedekt. In foarbyld foar seis wiken wurdt jûn yn 'e learaarboarne "Water Lilies."

   De groei fan 'e folchoarder dy't it bedekte gebiet beskriuwt is eksponentiell.

   Hoefolle kinne se drage?

   2D -oerflakgebieten groeie kwadratysk mei de lingte fan 'e kanten, wylst 3D -items kubysk kinne groeie (ie oant de krêft fan trije). Dêrom is it gewicht dat in skelet kin drage proporsjoneel oannommen dat alle kanten lineêr groeie, in kubike folchoarder groeit rapper dan in kwadratyske.

   In ferheging fan 'e hichte fan in bist kin allinich wurde berikt troch it skelet fan dat dier te meitsjen fan in materiaal dat hurder en sterker is dan foar lytsere bisten, of troch de grutte fan' e bisten fan it dier te fergrutsjen. Fanwegen it lytse gewicht fan in mier, is it skelet (en spieren) sterk genôch om tsien oant fyftich kear har eigen gewicht te dragen, wylst itselde net jildt foar minsken. Tink oan it gewicht fan in gebou dat wurdt stipe troch in pylder. As de boppeste ferdjippings te swier binne foar de stiennen pylder, begjint it te barsten en te krummeljen. Foar in unifoarm materiaal is it gewicht dat it kin drage proporsjoneel mei it dwerstrochsneedgebiet. Dus as jo alle diminsjes fan it gebou ferdûbelje, nimt it gewicht mei 8 kear ta, de pylderkapasiteit sil mar fjouwer kear omheech gean.

   Dit kin ek yllustrearre wurde troch it beskôgjen fan in mûs dy't by in liftas falt. Troch syn lytse gewicht kin it oerlibje, wylst gruttere bisten dat net soene. (Foarbyld oanpast fan TW Körner, The Pleasures of Counting, Cambridge University Press, 1996)

   Folje de Sequences

   De sekwinsjes wurde as folgjend fuortset, mei de respektivelike groeifunksjes jûn tusken heakjes:

   • 2, 2, 2, 2, 2, 2 (2)
   • 3, 6, 9, 12, 15, 18, 21 (3 xn)
   • 4, 9, 16, 25, 36, 49 ((n + 1) 2)
   • 2, 5, 10, 17, 26, 37, 50
   • 64, 96, 112, 120, 124, 126, 127

   De earste folchoarder groeit stadichst (syn groeifunksje is gewoan in konstante) wylst de tredde folchoarder fluchst groeit (de groeifunksje is kwadratysk). De fjirde folchoarder hat ek in kwadratyske groeifunksje en groeit dus mei deselde snelheid, mar har yndividuele items sille altyd leger wêze dan dy fan 'e tredde folchoarder.

    

   

2. Stel it ûnderwerp foar oan 'e studinten troch it Reward Game mei har te spyljen, dat wurdt beskreaun yn' e learaarboarne "Groepspultsjes." It spultsje bestiet út it jaan fan beleanningen, yn 'e foarm fan lytse items, oan' e studinten. It spul wurdt hjir útlein mei rys as foarbyld, mar it wurket like goed foar oare lytse beleannings. Rys wurdt yn rûnen jûn. It doel fan it spul is om safolle rys as mooglik te krijen. De hoemannichte rys jûn yn elke ronde wurdt bepaald troch ien fan twa beleanningstrategyen:
   Option 1: Elke rûnte sil in teelepel rys wurde útdield.
   Option 2: Yn 'e earste omloop is de beleanning mar ien riskorn. Dan, yn elke opienfolgjende ronde, wurdt de útjûne hoemannichte rys ferdûbele.
   • Lit elke studint ien fan 'e beleanningsstrategyen kieze en de studinten groepearje neffens de kar dy't se hawwe makke.
   • Fertel de beleannings rûn foar rûn foar elke groep. Jo kinne yn elke groep in studint beneame om te helpen de rys út te rekkenjen. Tink derom dat oan 'e ein in krekte telling fan korrels net wichtich is.
   • Nei de earste fjouwer omlopen, freegje de studinten de kumulative beleanning te fergelykjen. Doch itselde nei acht en tolve rûnen. Besprek dan de útkomst fan it spul mei de studinten.
   • Studinten moatte in yntuïtyf begryp krije fan 'e ferskate groeisnelheden. Dit kin ek wurde besibbe oan 'e tanimming fan rekkenkrêft fan moderne mikroprosessors. Neffens Moore's Law ferdûbelet it oantal transistors dat op in chip kin wurde pleatst sawat elke twa jier. De studinten kinne wurde frege te tinken oer de gefolgen fan dizze observaasje en oft it mooglik is dat dizze groei folle langer trochgiet.
3. Spielje it Number Guessing Game útlein yn 'e learaarboarne "Groepspultsjes." De oplossing hjirfoar wurdt hjirûnder werjûn. It doel fan it spul is om in nûmer te rieden mei sa min mooglik besykjen. It spul wurdt earst spile mei de heule klasse, en dan wurde de studinten yn pearen set om har eigen strategyen te ûndersiikjen om it spultsje op te lossen. Fertel de studinten om op te stean. Tink oan in nûmer tusken 1 en 50 en fertel it net oan 'e studinten. Se meie no allinich fragen stelle lykas "Is it 37?" of "Is it 20?" en jo meie allinich antwurdzje mei "ja" as "nee" oant se it juste nûmer fine. In studint dy't in fraach stelt dy't liedt ta in "nee" antwurd sil moatte sitten gean en kin net mear fragen stelle oant it spultsje is foltôge. Tink derom dat alle studinten miskien sitten foardat it spultsje is foltôge. Yn dit gefal kinne jo beslute it spultsje nochris te spyljen en te besprekken wêrom't it net wurke en dat mei dit soarte fragen yn 't minste gefal 50 besykjen fereaske binne.
   
   De biseksje metoade In optimale strategy foar it benaderjen fan it nûmer -riedspul is de metoade foar biseksje: Begjin mei te freegjen "Is it (strikt) grutter dan 50?" As it antwurd "ja" is, gean dan troch mei "Is it grutter dan 75?", As net, freegje "Is it grutter dan 25?" Trochgean op dizze manier om altyd nei it middelste nûmer te freegjen oant d'r mar ien opsje oer is. Bygelyks:
   • (It nûmer is 54)
   • Is it grutter dan 50? Ja
   • Is it grutter dan 75? Nee
   • Is it grutter dan 63? Nee
   • Is it grutter dan 57? Nee
   • Is it grutter dan 54? Nee
   • Is it grutter dan 52? Ja
   • Is it grutter dan 53? Ja

   Dat nei 7 fragen is it dúdlik dat it nûmer 54 wêze moat. (D'r binne gefallen wêryn mar 6 fragen nedich binne. Eins is it gemiddelde oantal fragen log 100 = 6.64.)

   Dit is in optimale metoade, om't by elke fraach de set mooglike nûmers is ferdield yn twa sawat gelikense dielen, wêrfan ien it fereaske nûmer befettet. Yn feite is foar dit probleem elke metoade dy't de mooglike nûmers per fraach halveret optimaal. In oare oplossing soe wêze om fragen te stellen lykas "Is it getal te dielen mei 2?"

   Opsjoneel: Fyn de kompleksiteit

   De kompleksiteit fan 'e biskesjemetoade is logaritmysk, ie fan folchoarder O (log N). Dit is in gefolch fan halvering fan de mooglike nûmers by elke fraach. As alle heule getallen binne tastien, dan kin gjin metoade it probleem yn definitive tiid oplosse.

4. Stel de studinten foar om algoritmen te sortearjen troch de ynstruksjes te folgjen op it wurkblêd foar studinten "Algoritmen sortearje", dws de kaarten útdiele en de studinten yn 'e foarstelde groepsgrutte sette. De oplossing ferskynt hjirûnder:
   

   Oplossing

   Bubble Sortearje As it dek net wurdt sorteare, sille d'r teminsten twa opienfolgjende kaarten wêze dy't net yn 'e juste folchoarder binne. It algoritme sil dizze twa kaarten úteinlik ruilje. Dêrom, as d'r net mear kaarten te wikseljen binne, einiget it algoritme en wurdt it dek sorteare. Bubble Sort hat it foardiel dat it heul ienfâldich is te ymplementearjen, mar it is net sa effisjint as mear avansearre sorteringsalgoritmen lykas fusearje sortearje (sjoch ûnder). De kompleksiteit fan runtiid fan borrelsorte foar n kaarten is kwadratysk, as O (n2).Faster sortearalgoritmen

   Wylst de kompleksiteit fan 'e runtime kwadratysk is, besteane d'r bettere metoaden. Bygelyks merge sort hat in run time complexiteit fan O (n log n) foar n kaarten. In nijsgjirrich skaaimerk fan merge sort is dat de struktuer it parallelisearret. In oar algoritme mei runtime -kompleksiteit O (n log n) dy't faaks wurdt brûkt by it oefenjen fan rappe sortearring. It presteart oer it algemien goed, hoewol de kompleksiteit fan 'e rintiid kwadratysk is en dus slimmer dan dy fan fúzje -soart. It is ek gewoan om hybride ferzjes fan ferskate sorteeralgoritmen te brûken om oan te passen oan spesifike problemen. Foar in ôflieding fan dizze resultaten sjoch TH Cormen et al., Introduction to Algorithms.

   Foar sortearjen basearre op it fergelykjen fan yndividuele items, is d'r gjin metoade mei in kompleksiteit fan 'e minste tiid run tiid better dan O (n log n) dy't parallelle operaasjes net eksploiteart, lykas fusearje fan ferskate stapels kaarten tagelyk. Dit komt om't n kaarten op nn ferskate manieren kinne wurde besteld, en elke ferliking kin it helte fan it oantal mooglike bestellingen helje, wat liedt ta in kompleksiteit fan O (log (nn)) = O (n log n).

5. Opsjoneel: Lit studinten de studintboarne "Algoritmen" lêze yn 'e seksje "Eftergrûnkonsepten" om de terminology te learen dy't wurdt brûkt yn kompjûterwittenskip.
6. Foar mear ynhâld oer it ûnderwerp, sjoch de seksje "Dieper graven".

Avansearre opsjes

Avansearre studinten kinne in ferlykjend essay skriuwe oer ferskate sorteermethoden en de kritearia foar ferklearjen foar it foarkommen fan de iene metoade boppe de oare. Avansearre studinten kinne wurde frege om arguminten te jaan fan 'e berekkeningskompleksiteit fan' e beskôge algoritmen en wêrom de prestaasjes fan algoritmen foar fergeliking sortearje yn prinsipe beheind is.

De les kin yn mar 1 lesperioade dien wurde foar âldere studinten. Om studinten lykwols te helpen har te fielen en te soargjen foar sukses fan studinten (spesjaal foar jongere studinten), splitst de les yn twa perioaden, wêrtroch studinten mear tiid hawwe om te brainstormen, ideeën te testen en har ûntwerp te finalisearjen. Doch it testen en debrief yn 'e folgjende lesperioade.

Wat is in algoritme?

In kompjûter kin wurde brûkt om in oerfloed fan taken út te fieren dy't ús kinne helpe mei ús wurk. Soms binne dizze taken maklik te beskriuwen yn wurden, lykas "sortearje dizze kaartkaart", of "de fluchste manier fine fan Parys nei New York". Foar in kompjûter kinne dizze taken lykwols heul lestich wêze om op te lossen. Yntern kin in komputer allinich leaver prestearje primitive operaasjes en allinich har juste regeling lost in probleem op. Sa'n regeling wurdt in neamd algoritme. Om't elke primitive operaasje wat tiid duorret (in pear nanosekonden yn in moderne komputer), fereasket in algoritme in bepaalde rintiid om syn taak te foltôgjen.

Wêrom binne guon algoritmen better dan oaren?

Elke taak fereasket in spesjaal ûntworpen algoritme dat it kin oplosse. In kaartsje sortearje kin net dien wurde mei in algoritme dat is ûntworpen om it koartste paad te finen tusken twa stêden. Ek frij yntuïtyf, it sortearjen fan in dek fan 200 kaarten duorret langer dan sortearje mar 52 kaarten (of yn it triviale gefal, 2 kaarten). Dêrom hinget de rintiid ôf fan it probleem en de grutte (komputerwittenskippers sprekke fan in probleem eksimplaar).

Algoritmen moatte ûnôfhinklik wurde fergelike fan it probleemeksemplaar (oars soe it bêste algoritme altyd wêze om it antwurd dat earder berekkene is gewoan direkt te jaan.) Dit is wêr't it konsept fan 'e groei fan in folchoarder nuttich komt: De grutte fan it probleem kin wurde beskôge as de parameter n yn in folchoarder dy't spesifyk is foar it algoritme. D'r binne dêrom algoritmen fan ferskate kompleksiteit, oerienkomt mei de folchoarder dy't se beskriuwt. Algoritmen wurde dan fergelike troch de groei fan 'e sekwinsjes te fergelykjen. Dêrom is in algoritme fan kwadratyske kompleksiteit better dan in algoritme fan eksponentiële kompleksiteit.

Kompleksiteit - it is nuttich

De effisjinsje fan algoritmen is krúsjaal foar in oerfloed fan hjoeddeistige computingapplikaasjes. Guon problemen binne heul lestich op te lossen, om't de ienige bekende algoritmen dy't se oplosse in heul hege kompleksiteit hawwe.

In algemien bekend foarbyld fan hege kompleksiteit is it probleem fan reizgjende ferkeaper (TSP). Yn dit probleem wol in keapman saken dwaan yn in set stêden. Hy wol de koartst mooglike rûte fine tusken dizze stêden sûnder mear dan ien kear in stêd te besykjen, en hy wol oan 'e ein fan syn reisplan weromkomme nei syn startstêd. Dit effisjint oplosse soe heul nuttich wêze foar de tawizing fan rûtes foar fleantugen, it plannen fan taken op masines en sels de fabrikaazje fan mikroprosessors.

Wylst de kompleksiteit fan 'e TSP in effisjinte oplossing fan dizze problemen foarkomt, kin foar guon applikaasjes hege kompleksiteit sels winsklik wêze. As in fersifere berjocht wurdt ferstjoerd, soe it heul lestich moatte wêze om by de ferstjoerde ynformaasje te kommen sûnder wat dielde geheim te witten. Yn dit gefal is de fersifering sa ûntworpen dat de ûntsiferje in heul hege kompleksiteit hat en sadwaande ôfharkjen wurdt foarkommen. Feilige kommunikaasje soe net mooglik wêze sûnder de hege kompleksiteit fan ûntsiferjen. Dizze foarbylden en tal fan oaren litte sjen dat it kennen fan 'e kompleksiteit fan in probleem heul nuttich is foar berekkenjen en fierder.

Internet Connections

• Complexity Zoo: (https://complexityzoo.uwaterloo.ca/Complexity_Zoo#sthash.1Gnn1E1Z.dpuf)
• P vs NP Probleem
• Moore's wet
• Algorithm Analysis: (http://www.londoninternational.ac.uk/sites/default/files/computingsamples/co2226_vol2_ch1.pdf#sthash.1Gnn1E1Z.dpuf)
• ITEA Standards for Technological Literacy
• Nasjonale standerts foar wittenskiplik ûnderwiis: (http://www.nsta.org/publications/nses.aspx)
• Skalearring

Recommended Reading

• Groei fan sekwinsjes en sortearalgoritmen: ynlieding foar algoritmen troch TH Cormen et al. (ISBN: 0070131511)
• Dimensional Analysis: The Pleasures of Counting troch TW Körner (ISBN: 0521568234)

Skriuwaktiviteit

Fergelykje ferskate sorteermethoden en ferklearje wêrom jo de ien leaver wolle as de oare. Skriuw in koarte tekst oer it belang fan komputaasjekompleksiteit yn kryptografy.

Rjochting op kurrikulumkaders

Noat: Lesplannen yn dizze searje binne ôfstimd op ien of mear fan 'e folgjende sets standerts:

• S. Standertnormen foar wittenskip (http://www.nap.edu/catalog.php?record_id=4962)
• S. Science Standards foar de folgjende generaasje (http://www.nextgenscience.org/)
• Standards foar International Technology Education Association foar technologyske geletterdheid (http://www.iteea.org/TAA/PDFs/xstnd.pdf)
• S. Prinsipes en noarmen foar leararen fan wiskunde foar skoalwiskunde (http://www.nctm.org/standards/content.aspx?id=16909)
• S. Common Core State Standards for Mathematics (http://www.corestandards.org/Math)
• Computer Science Science Teachers Association K-12 Computer Science Standards (http://csta.acm.org/Curriculum/sub/K12Standards.html)

Prinsipes en noarmen foar skoalwiskunde

Algebra Standert

As resultaat fan aktiviteiten moatte alle studinten har ûntwikkelje

• Patroanen, relaasjes en funksjes begripe.
• Brûk wiskundige modellen om kwantitative relaasjes foar te stellen en te begripen.

Probleemoplossing Standert

As resultaat fan aktiviteiten moatte alle studinten har ûntwikkelje

• Tapasse en oanpasse in ferskaat oan passende strategyen om problemen op te lossen.
• Monitor en reflektearje oer it proses fan wiskundige probleemoplossing.

Common Core State Standards for Mathematics Grades 9-12 (leeftiden 14-18)

Algebra Standert

• Redenearje mei fergelikingen en ûngelikens
• Los fergelikingen en ûngelikens op yn ien fariabele
• Math.Content.HSA-REI.B.3Los lineêre fergelikingen en ûngelikens op yn ien fariabele, ynklusyf fergelikingen mei koeffisienten fertsjintwurdige troch letters.

funksjes Standert

• Bouwen funksjes
• Bou in funksje dy't in relaasje modeleart tusken twa hoemannichten
• Math.Content.HSF-BF.A.2Skriuw rekenkundige en geometryske sekwinsjes sawol rekursyf as mei in eksplisite formule, brûk se om situaasjes te modellerjen, en oersette tusken de twa foarmen.
• Lineêre, kwadratyske, en eksponentjele modellen
• Konstruearje en fergelykje lineêre, kwadratyske, en eksponinsjele modellen en lossen problemen op
• Math.Content.HSF-LE.A.1Ingunderskiede tusken situaasjes dy't kinne wurde modeleare mei lineêre funksjes en mei eksponentjele funksjes.
• Math.Content.HSF-LE.A.1cHerken situaasjes wêryn in kwantiteit groeit of ferfalt mei in konstant persintaazjetarief per ienheidsinterval relatyf oan in oar.

 Noarmen foar technologyske geletterdheid - Alle leeftiden

         De natuer fan technology

• Standert 1: Studinten sille in begrip ûntwikkelje fan 'e skaaimerken en omfang fan technology.
• Standert 2: Studinten sille in begrip ûntwikkelje fan 'e kearnbegripen fan technology.
• Standert 3: Studinten sille in begryp ûntwikkelje fan 'e relaasjes tusken technologyen en de ferbiningen tusken technology en oare stúdzjerjochten.

De ûntworpen wrâld

• Standert 17: Studinten sille in begrip ûntwikkelje fan en kinne ynformaasje- en kommunikaasjetechnologyen selektearje en brûke.

CSTA K-12 Computer Science Standards Grades 6-9 (leeftyd 11-14)

5. 2 nivo 2: Computer Science and Community (L2)

• Computational Thinking (CT)

3. Definearje in algoritme as in folchoarder fan ynstruksjes dy't kinne wurde ferwurke troch in kompjûter.
4. Evaluearje manieren wêrop ferskate algoritmen kinne wurde brûkt om itselde probleem op te lossen.
5. Meitsje sykjen en sortearjen fan algoritmen.
6. Brûk fisuele foarstellingen fan probleemstatus, struktueren en gegevens (bgl. Grafiken, diagrammen, netwurkschema's, streamdiagrammen).
7. Ynteraksje mei ynhâldspesifike modellen en simulaasjes (bgl. Ekosystemen, epidemyen, molekulêre dynamyk) om learen en ûndersyk te stypjen.

• Gearwurking (CL)

3. Gearwurkje mei leeftydsgenoaten, saakkundigen en oaren mei help fan gearwurkingspraktiken lykas pearprogrammering, wurkje yn projektteams, en meidwaan oan groepsaktive learaktiviteiten.
4. Tentoanstellings nedich foar gearwurking: nuttige feedback leverje, feedback yntegrearje, meardere perspektiven begripe en akseptearje, sosjalisaasje.

• Computing Practice & Programming (CPP)

4. Demonstrearje in begryp fan algoritmen en har praktyske tapassing.

CSTA K-12 Computer Science Standards Grades 9-12 (leeftyd 14-18)

5.3 Niva 3: Konsepten tapasse en oplossingen meitsje foar echte wrâld (L3)

5.3.A Kompjûterwittenskip yn 'e moderne wrâld (MW)

• Computational Thinking (CT)

3. Ferklearje hoe't folchoarder, seleksje, iteraasje en rekursje boustiennen fan algoritmen binne.
4. Brûk modellering en simulaasje om natuerlike ferskynsels foar te stellen en te begripen.

5.3.B Computer Science Concepts and Practices (CP)

• Computational Thinking (CT)

5. Gebrûk fan gegevensanalyse om it ferstean fan komplekse natuerlike en minsklike systemen te ferbetterjen.

9. Analysearje gegevens en identifisearje patroanen fia modellering en simulaasje.

De groei fan sekwinsjes

 Pompeblêden

Op in fiver is d'r in inkelde wetterlelie. Elke wike ferdûbelet it oantal wetterlelies op 'e fiver. De fiver is nei 10 wiken folslein bedekt mei wetterlelies. Nei hoefolle wiken is mar de helte fan 'e fiver bedekt mei wetterlelies? Ferklearje jo redenearring.

Hoefolle kinne se drage?

It gewicht dat in skelet kin drage is proporsjoneel mei syn dwerstrochsneedgebiet. It gewicht fan in bist is evenredich mei syn folume. Wêrom tinke jo dat in mier tsien oant fyftich kear har eigen gewicht kin drage, wylst in minske har eigen gewicht amper kin drage? (Hint: Fergelykje de groei fan in gebiet en in folume.)

Folje de Sequences

Fyn de folgjende twa eleminten yn elk fan 'e folgjende sekwinsjes.

• 2, 2, 2, 2, ___, ___
• 3, 6, 9, 12, 15, ___, ___
• 4, 9, 16, 25, ___, ___
• 2, 5, 10, 17, 26, ___, ___
• 64, 96, 112, 120, 124, ___, ___

Foar de earste trije sekwinsjes fine jo ek har respektivelike groeifunksje (yn termen fan n).

Hokker folchoarder groeit it stadichst?

Hokker sekwinsjes groeie it rapst?

In nûmer rieden spultsje

Wurkje tegearre mei jo buorman. Ien fan jo moat tinke oan in nûmer tusken 1 en 100. Fertel it noch net oan jo partner. It doel fan jo partner is om dat oantal yn sa min mooglik besykjen te rieden. Jo kinne allinich fragen beantwurdzje mei "ja" as "nee". As jo ​​partner ienris it juste nûmer hat fûn, wikselje rollen.

De biseksje metoade

Jo meie allinich fragen stelle lykas "Is it nûmer grutter dan 20?" of "Is it nûmer grutter dan 54?" Wat is de bêste strategy dy't jo kinne fine yn dit gefal? Hoefolle besykjen hawwe jo nedich yn it slimste gefal?

Ferklearje yn in pear wurden wêrom jo metoade optimaal is.

Opsjoneel: Fyn de kompleksiteit

Kinne jo in folchoarder fine dy't beskriuwt hoefolle fragen yn it slimste gefal binne fereaske as nûmers fan 1 oant N tastien binne? It antwurd wurdt it bêste útdrukt yn grutte-O-notaasje. (Hint: Besykje it logaritme.) Wat bart der as alle heule getallen binne tastien?

As jo ​​mear witte wolle oer it finen fan de kompleksiteit, kinne jo it boek besjen fan TH Cormen et al., Introduction to Algorithms of op 'e webside http://www.londoninternational.ac.uk/current_students/programme_resources/cis/pdfs /subject_guides/level_2/cis226_vol2/cis226_chap1.pdf

Algoritmen sortearje

Jo sille no nei in pear sorteermethoden sjen. Jo learaar sil jo kaarten jaan en jo sille twa ferskillende sorteermethoden leare.

Om it gedrach fan in kompjûter te imitearjen, kinne jo allinich bepaalde ienfâldige operaasjes útfiere: Jo meie twa kaarten tagelyk besjen, fergelykje se en ferpleatse se wêr't jo wolle, ôfhinklik allinich fan 'e wearden fan' e twa kaarten. Sokke operaasjes kinne omfetsje it wikseljen fan de kaarten, it ynstekken fan de iene kaart foar de oare, ensfh. Fansels kinne jo ek nije hulppunten kaarten iepenje.

Jo meie lykwols net gewoan nei alle kaarten sjen, har wearde ûnthâlde en se direkt yn 'e juste posysje pleatse.

Bubble Sortearje

Meitsje yn groepen fan trije. Elke groep krijt acht kaarten. Shuffle de kaarten en pleatst de kaarten mei it gesicht nei ûnderen op 'e tafel.

In ienfâldige metoade foar sortearjen is bubbelsorte. Tapasse de folgjende stappen op jo 8 kaarten:

1. Sjoch nei de earste twa kaarten en fergelykje se
2. Wikselje de kaarten (as nedich) sadat se yn tanimmende folchoarder binne
3. Sjoch no nei de twadde en tredde kaart en wikselje se as se net yn tanimmende folchoarder binne
4. Trochgean mei dwaan oant jo de sânde en achtste kaart berikke. Wikselje se as it nedich is
5. Herhelje no stappen 1-4 oant jo gjin swaps mear hoege te dwaan.

De earste pear swaps wurde yllustrearre yn 'e figuer rjochts. De earste twa kaarten moatte wurde wiksele, yn it sintrum steane de kaarten al yn 'e

korrekte folchoarder en de "8" en de "3" moatte wurde wiksele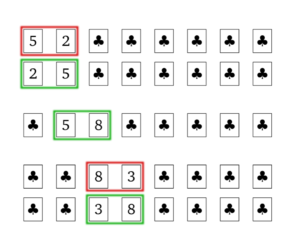 wer.

Nei it foltôgjen, draai alle kaarten om en kontrolearje oft se binne sorteare. Ferklearje yn in pear wurden wêrom dizze metoade wurket.

Fakultatyf: Krij yn groepen fan fiif oant tsien en fyn jo eigen sorteermetoade mei allinich de tastiene operaasjes lykas hjirboppe útlein. Kinne jo better wurde dan bubbelsoart? Wêrom / wêrom net?